মন্টি হল প্রবলেম - আপনি হলে কি করতেন?
Jun 4, 2014
সেটআপ
ধরে নিন আপনি একটি গেম শো তে অংশগ্রহণ করছেন। শো এর হোস্ট আমি। আমি আপনার সামনে তিনটি দরজা রাখলাম। দরজা তিনটির মধ্যে একটির পিছনে একটি গাড়ি আছে। বাকি যে দুটো দরজা আছে তাদের পিছনে কোন ফালতু জিনিস রাখা আছে। ধরা যাক দুটো ছাগল রাখা আছে। মূল ব্যাপারটা হল একটি দরজার পিছনে বাকি দুটোর তুলনায় অনেক মূল্যবান কিছু আছে যেটি আপনি অবশ্যই জিতে নিতে চান। কিন্তু আপনি জানেন না কোন দরজার পিছনে কি আছে। আর যেহেতু আমি হোস্ট, আমি অবশ্যই জানি কোনটার পিছনে কি আছে! এই হল পুরো গেমের সেটআপ।
এখন গেমপ্লেতে আসা যাক। আপনাকে আমি বললাম তিনটি দরজার মধ্যে থেকে যেকোন একটি দরজা সিলেক্ট করতে। এই কাজে আপনার পূর্ণ স্বাধীনতা আছে। যেই দরজা আপনি সিলেক্ট করবেন সেটার পিছনের জিনিসটি আপনাকে উপহার হিসেবে দেওয়া হবে। অবশ্যই আপনি গাড়িটি বাসায় নিয়ে যেতে চান! তাই অনেক চিন্তাভাবনা করে যেকোন একটি দরজা সিলেক্ট করলেন। এখন একটা ছোট্ট টুইস্ট। আপনি আপনার পছন্দের দরজা বেছে নেওয়ার পর আমি বাকি দরজা দুটোর মধ্যে একটি খুলে দিব। অবশ্যই আমি এমন একটা দরজা খুলব যেটার পিছনে গাড়ি নেই। যদি দুটোর কোনটার পিছনেই গাড়ি না থাকে তাহলে আমি যেকোনোটা একটি খুলে দিব। এখন তাহলে দুটো দরজা বাকি থাকল যার মধ্যে একটি আপনার পছন্দের। আপনাকে এখন আমি দুটো অপশন দিলাম। এক, আপনি যেটি পছন্দ করেছেন সেটিই নিবেন। দুই, আপনি অপর যে দরজাটি আছে সেটি নিবেন।
প্রশ্ন হল আপনার এখন কি করা উচিত? যেই দরজা বেছে নিয়েছেন সেটিতেই থাকা, নাকি পরিবর্তন করে অপর দরজাটি বেছে নেওয়া? কোনটা করলে আপনার গাড়ি পাওয়ার সম্ভাবনা বাড়বে? আদৌ কি সম্ভাবনা বাড়া কমার কোন ব্যাপার আছে?
কিছুক্ষণ চিন্তা করুন। যৌক্তিক পদ্ধতিতে চিন্তা করুন। সিলেকশন পরিবর্তন করলে কি হবে, আর না করলে কি হবে। কিছুক্ষণ ভেবে তারপর লেখার বাকি অংশ পড়ুন।
মন্টি হল প্রবলেম
আপনাকে এখানে যে সমস্যাটার সম্মুখীন হতে হল এটি অত্যন্ত বিখ্যাত এবং সুন্দর একটা প্রবলেম যেটির নাম “মন্টি হল প্রবলেম”। প্রবলেমটি প্রতিষ্ঠিত হয়েছে বিখ্যাত আমেরিকান গেম শো “Let’s make a deal” থেকে। অনুষ্ঠানের হোস্ট মন্টি হল এর নামানুসারে প্রবলেমটির নামকরণ করা হয়। প্রবলেমটি প্রথম উত্থাপিত হয় ১৯৭৫ সালে “American Statistician” নামক জার্নালে।
প্রবলেমটা বিশ্লেষণ করতে কিছুটা প্রোবাবিলিটি/সম্ভাব্যতার জ্ঞান প্রয়োজন। একথা শুনে অনেকে ভড়কে যেতে পারে, লেখাটি পড়া বাদ দিতে পারে। তাদের জন্য বলি, এই জ্ঞান তেমন আহামরি কিছুই না। সাধারণ জ্ঞান থেকেই সবকিছু বোঝা সম্ভব। সাধারণ জ্ঞানটাকেই একটু বৈজ্ঞানিক একটা নাম দেওয়া হয়েছে “সম্ভাব্যতা”, আর কিছুই না। তাই ভয় পাওয়ার কিছু নেই, পড়তে থাকুন!
প্রাথমিক বিশ্লেষণ
গেমটি যখন শুরু হল তখন আপনার সামনে তিনটি দরজা ছিল। কোন দরজার পিছনে কি আছে সেই ব্যাপারে যেহেতু আপনার কাছে কোন তথ্য নেই অতএব আপনি যেই দরজাই বেছে নিচ্ছেন না কেন সেটি সম্পূর্ণরূপে র্যান্ডম। আপনাকে তিনটি দরজার মধ্যে থেকে একটি বেছে নিতে হয়েছে। তিনটির মধ্যে যেকোনো একটির পিছনে গাড়ি থাকতে পারে। তাই কোন একটি দরজার পিছনে গাড়ি থাকার সম্ভাবনা ১/৩ (এক-তৃতীয়াংশ)। যেহেতু প্রতিটা দরজার ক্ষেত্রেই সম্ভাবনা ১/৩ তাই প্রথমে কোনটা বেছে নিচ্ছেন তাতে তেমন কিছুই যায় আসে না।
এবার পরবর্তি অংশে আসা যাক। যখন আমি একটা দরজা খুলে দিলাম তখন বাকি থাকছে দুটো দরজা। যেহেতু দুটো দরজা আছে এবং তার মধ্যে একটির পিছনে গাড়ি আছে, অপরটির পিছনে নেই, তাই এখানে কোন একটি দরজার পিছনে গাড়ি থাকবে তার সম্ভাবনা ১/২। যেহেতু দুটি দরজার প্রত্যেকটির ক্ষেত্রেই সম্ভাবনা ১/২ অতএব আপনি এখন দরজা পরিবর্তন করুন আর নাই করুন, একই কথা! উভয় ক্ষেত্রে গাড়ি পাওয়ার সম্ভাবনা একই থাকছে, ১/২!
কিন্তু না, একই থাকবে না। এখানেই প্রব্লেমটার মজা! কেন দেখা যাক।
স্বজ্ঞাবিরোধি ফল (Counter intuitive result)
এই প্রবলেমটা যখন প্রথম সবার সামনে আসে তখন অনেক বড় বড় গণিতবিদেরাও বলেছিলেন যে প্রথমে সম্ভাবনা ১/৩ থাকবে এবং পরবর্তিতে সেটি ১/২ হবে। কিন্তু একটি বিষয় খেয়াল রাখা উচিত, অনুষ্ঠানের হোস্ট যিনি, তিনি কিন্তু এখানে একটি বাড়তি তথ্য যোগ করেছেন। তিনি জানেন কোথায় গাড়িটি আছে। গাড়িটি নেই এমন একটি দরজা তিনি খুলে দেখিয়েছেন। যেহেতু তিনি একটি তথ্য দিয়ে দিয়েছেন, তাই সম্ভাব্যতার পরিবর্তন ঘটবে। এখন প্রশ্ন হল কিভাবে পরিবর্তন ঘটবে।
একদম সহজ প্রক্রিয়ায় চিন্তা করা যাক। প্রথমে যখন আপনাকে দরজা বাছাই করতে বলা হল, তখন কোন একটা দরজায় গাড়ি পাওয়ার সম্ভাবনা ছিল ১/৩। অর্থাৎ আপনি যে দরজাটি বাছাই করেছেন তার পিছে গাড়ি আছে এমনটি ঘটার সম্ভাবনা ১/৩। বিপরীতভাবে চিন্তা করলে, আপনি যে দরজাটি বাছাই করেছেন সেখানে গাড়ি না থাকার সম্ভাবনা ২/৩। যেহেতু সেখানে গাড়ি না থাকার সম্ভাবনা ২/৩ অতএব বাকি দুটো দরজার পিছনে গাড়িটি আছে এমনটি ঘটার সম্ভাবনা ২/৩। এখন আমি যখন একটি দরজা খুলে দিব, তখন আপনি নিশ্চিত হয়ে গেলেন যে ঐ দরজাটির পিছনে গাড়ি নেই। অতএব বাকি যে একটি দরজা থাকলো পূর্বের সেই ২/৩ সম্ভাবনা এখন সেটির উপর বর্তাবে। ফলে সেখানে গাড়ি থাকার সম্ভাবনা বেড়ে হবে ২/৩! ফলে দরজা পরিবর্তন করলে গাড়ি পাওয়ার সম্ভাবনা বেড়ে যাচ্ছে!
ব্যাপারটা শুরুতে হজম করা খুব কষ্টকর হলেও একটু চিন্তা করলেই ধরতে পারবেন। এমনটি হচ্ছে কারণ হোস্ট এখানে নতুন তথ্য যোগ করছে।
উদাহরণের মাধ্যমে একটু উপলব্ধি করার চেষ্টা করা যাক।
ধরে নিন আপনি ১ নাম্বার দরজাটি বেছে নিয়েছেন। কোন দরজার পিছনে কি আছে সেটার বিন্যাস তিন রকম হতে পারে, আর সেকারণে আপনি একটি দরজা বেছে নিয়ে যদি সেটিকেই রাখতে চান তাহলে মোট ঘটনা হতে পারে তিনরকম।
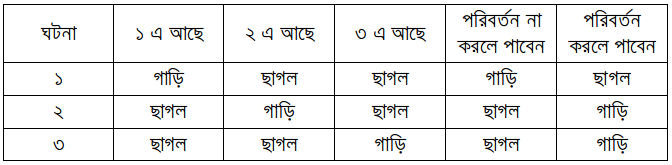
প্রথম ঘটনাটির সময় যা হবে, যেহতু আপনি যে দরজাটি নিয়েছেন সেটিতেই গাড়িটি আছে, অতএব হোস্ট বাকি দুটো দরজার যেকোনটি খুলে দিবে। এখন যদি আপনি পরিবর্তন না করেন, তাহলে গাড়ি পাবেন, আর যদি পরিবর্তন করেন, তাহলে পাবেন না। দ্বিতীয় এবং তৃতীয় ক্ষেত্রে যেটি হবে, আপনি যে দরজা নিয়েছেন সেটিতে যেহেতু ছাগল আছে, ফলে অপর দুটোর মধ্যে একটি মাত্র দরজার পিছে ছাগল থাকবে। হোস্ট যেহেতু গাড়িটি দেখাবেন না, অতএব তিনি বাধ্য ঐ একটি মাত্র দরজা খুলে দিতে। অপর যে দরজাটি থাকবে সেটিতে তাহলে অবশ্যই গাড়ি থাকবে। তাই দ্বিতীয় এবং তৃতীয় ঘটনায় পরিবর্তন করলে আপনি গাড়ি পাচ্ছেন।
দেখা যাচ্ছে, মোট তিনরকম ঘটনার মধ্যে আপনি যদি পরিবর্তন না করেন তাহলে একবার গাড়ি পাচ্ছেন, আর যদি পরিবর্তন করেন, তাহলে দুইবার গাড়ি পাচ্ছেন! অর্থাৎ পরিবর্তন না করলে সম্ভাবনা ১/৩, পরিবর্তন করলে সম্ভাবনা ২/৩, বেড়ে যাচ্ছে!
কি অদ্ভুত!
আসলেই ব্যাপারটা অনেক অদ্ভুত। কিন্তু হ্যাঁ, এটাই সত্য – গাণিতিকভাবে প্রমাণিত সত্য। পরিবর্তন করলে গাড়ি পাওয়ার সম্ভাবনা বেড়ে যাবে। তবে সম্ভাবনা বেড়ে যাওয়া মানে এটা নয় যে আপনি পরিবর্তন করলে নিশ্চিতভাবে গাড়ি জিতে নেবেন। সম্ভাবনা বেড়ে যাওয়া মানে যদি অনেকগুলো খেলা হয়, তাহলে তার প্রায় দুই-তৃতীয়াংশ খেলায় পরিবর্তন করলে গাড়ি পাওয়া যাবে।
অতএব এরপর থেকে কোন গেম শোতে গেলে একটু চিন্তা ভাবনা করে সিদ্ধান্ত নেবেন। সরল সাধারণ দৃষ্টিতে যেটি মনে হবে তেমনটি সবসময় সত্য নাও হতে পারে। বরং সজ্ঞাবিরোধি কিন্তু যৌক্তিক সিদ্ধান্ত অনেকক্ষেত্রেই জয় পরাজয়ের ফারাক গড়ে দিতে পারে। কেবল দরকার একটা যুক্তিবাদী মন এবং মুক্ত চিন্তার ইচ্ছা। মন্টি হল প্রবলেম তারই একটা দৃষ্টান্ত!
আরও জানতে